You’re minding your own business when some punk asks what the integral of $sin(x)$ means. Your options:

• Pretend to be asleep (except not in the library again)
• Canned response: “As with any function, the integral of sine is the area under its curve.”
• Geometric intuition: “The integral of sine is the horizontal distance along a circular path.”

Option 1 is tempting, but let’s take a look at the others.

Why “Area Under the Curve” is Unsatisfying

Describing an integral as “area under the curve” is like describing a book as a list of words. Technically correct, but misses the message and I suspect you haven’t done the assigned reading.

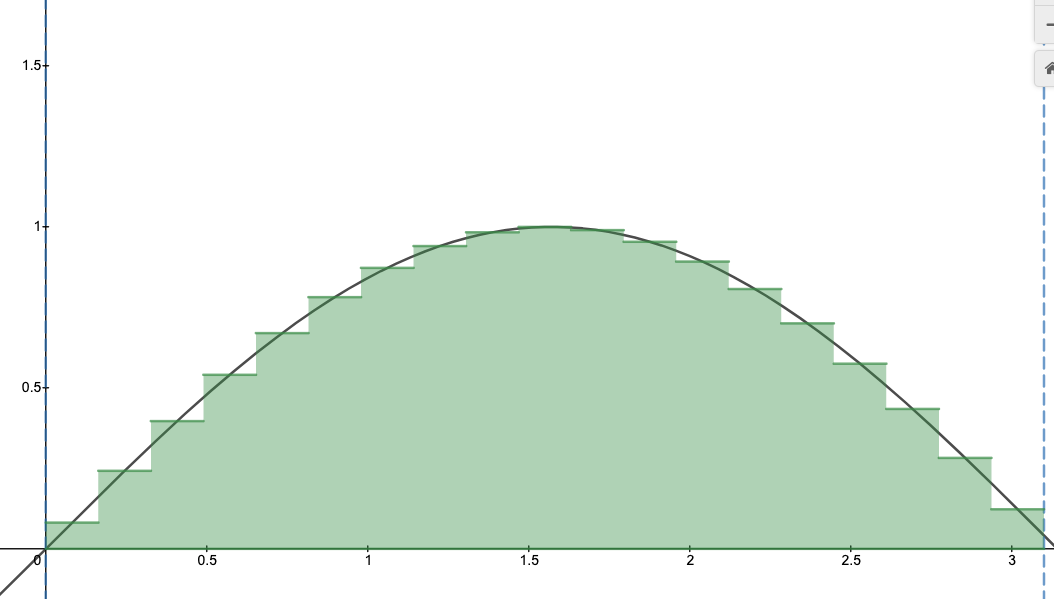
Unless you’re trapped in LegoLand, integrals mean something besides rectangles.

Decoding the Integral

My calculus conundrum was not having an intuition for all the mechanics.

When we see:

$int sin(x) dx$

We can call on a few insights:

• The integral is just fancy multiplication. Multiplication accumulates numbers that don’t change (3 + 3 + 3 + 3). Integrals add up numbers that might change, based on a pattern (1 + 2 + 3 + 4). But if we squint our eyes and pretend items are identical we have a multiplication.

• $sin(x)$ just a percentage. Yes, it’s also fancy curve with nice properties. But at any point (like 45 degrees), it’s a single percentage from -100% to +100%. Just regular numbers.

• $dx$ is a tiny, infinitesimal part of the path we’re taking. 0 to $x$ is the full path, so $dx$ is (intuitively) a nanometer.

Ok. With those 3 intuitions, our rough (rough!) conversion to Plain English is:

The integral of sin(x) multiplies our intended path length (from 0 to x) by a percentage

We intend to travel a simple path from 0 to x, but we end up with a smaller percentage instead. (Why? Because $sin(x)$ is usually less than 100%). So we’d expect something like 0.75x.

In fact, if $sin(x)$ did have a fixed value of 0.75, our integral would be:

$int text{fixedsin}(x) = int 0.75 dx = 0.75 int dx = 0.75x$

But the real $sin(x)$, that squirrelly rogue, changes as we go. Let’s see what fraction of our path we really get.

Visualize The Change in Sin(x)

Now let’s visualize $sin(x)$ and its changes:

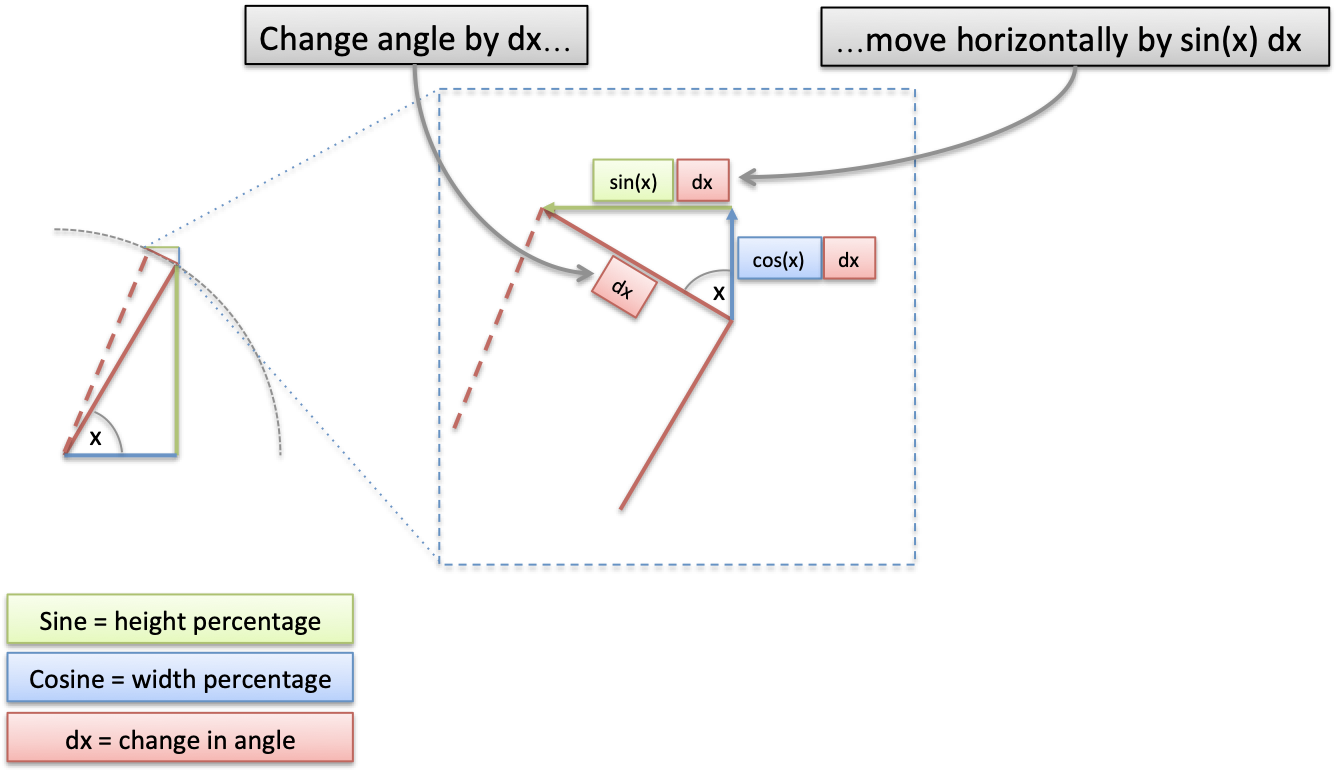
Here’s the decoder key:

• $x$ is our current angle in radians. On the unit circle (radius=1), the angle is the distance along the circumference.

• $dx$ is a tiny change in our angle, which becomes the same change along the circumference (moving 0.01 units in our angle moves 0.01 along the circumference).

• At our tiny scale, a circle is a a polygon with many sides, so we’re moving along a line segment of length $dx$. This puts us at a new position.

With me? With trigonometry, we can find the exact change in height/width as we slide along the circle by $dx$.

By similar triangles, our change just just our original triangle, rotated and scaled.

• Original triangle (hypotenuse = 1): height = $sin(x)$, width = $cos(x)$
• Change triangle (hypotenuse = dx): height = $sin(x) dx$, width = $cos(x) dx$

Now, remember that sine and cosine are functions that return percentages. (A number like 0.75 doesn’t have its orientation. It shows up and makes things 75% of their size in whatever direction they’re facing.)

So, given how we’ve drawn our Triangle of Change, $sin(x) dx$ is our horizontal change. Our plain-English intuition is:

The integral of sin(x) adds up the horizontal change along our path

Visualize The Integral Intuition

Ok. Let’s graph this bad boy to see what’s happening. With our “$sin(x) dx$ = tiny horizontal change” insight we have:

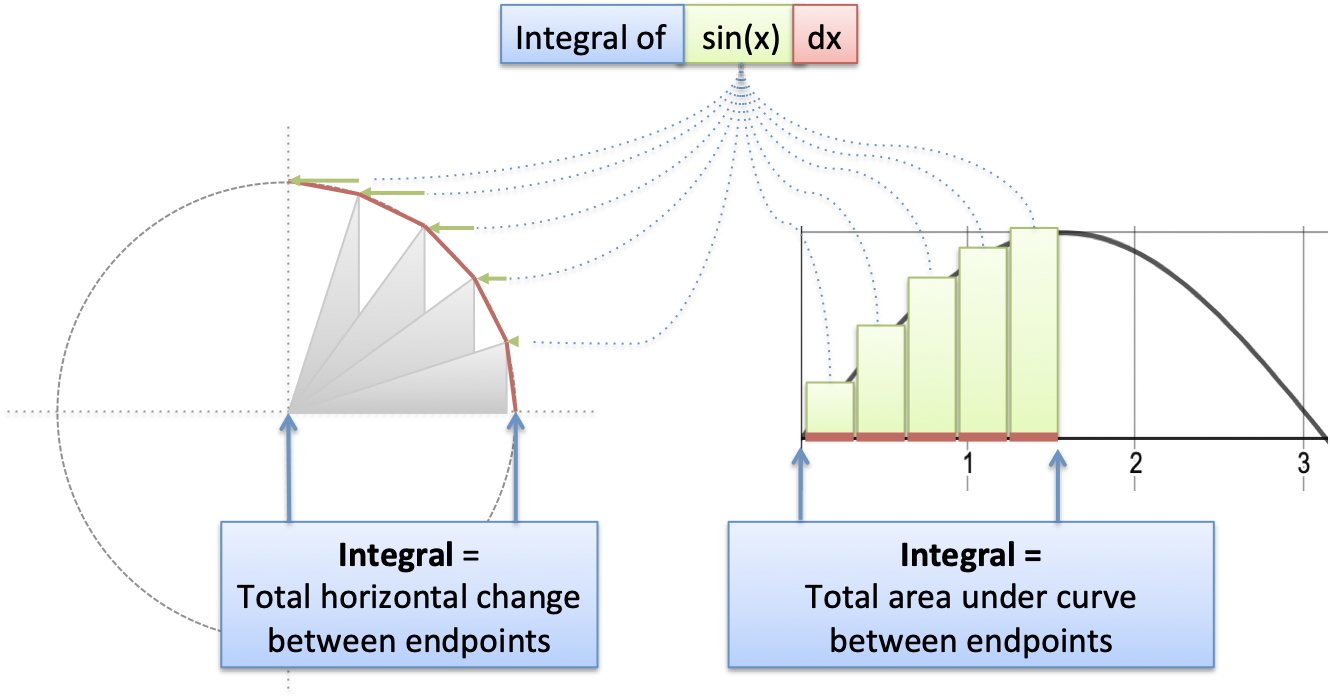
As we circle around, we have a bunch of $dx$ line segments (in red). When sine is small (around x=0) we barely get any horizontal motion. As sine gets larger (top of circle), we are moving up to 100% horizontally.

Ultimately, the various $sin(x) dx$ segments move us horizontally from one side of the circle to the other.

A more technical description:

$int_0^x sin(x) dx = text{horizontal distance traveled on arc from 0 to x}$

Aha! That’s the meaning. Let’s eyeball it. When moving from $x=0$ to $x=pi$ we move exactly 2 units horizontally. It makes complete sense in the diagram.

The Official Calculation

Using the Official Calculus Fact that $int sin(x) dx = -cos(x)$ we would calculate:

$ int_0^pi sin(x) dx = -cos(x) Big|_0^pi = -cos(pi) – -cos(0) = -(-1) -(-1) = 1 + 1 = 2$

Yowza. See how awkward it is, those double negations? Why was the visual intuition so much simpler?

Our path along the circle ($x=0$ to $x=pi$) moves from right-to-left. But the x-axis goes positive from left-to-right. When convert distance along our path into Standard Area™, we have to flip our axes:

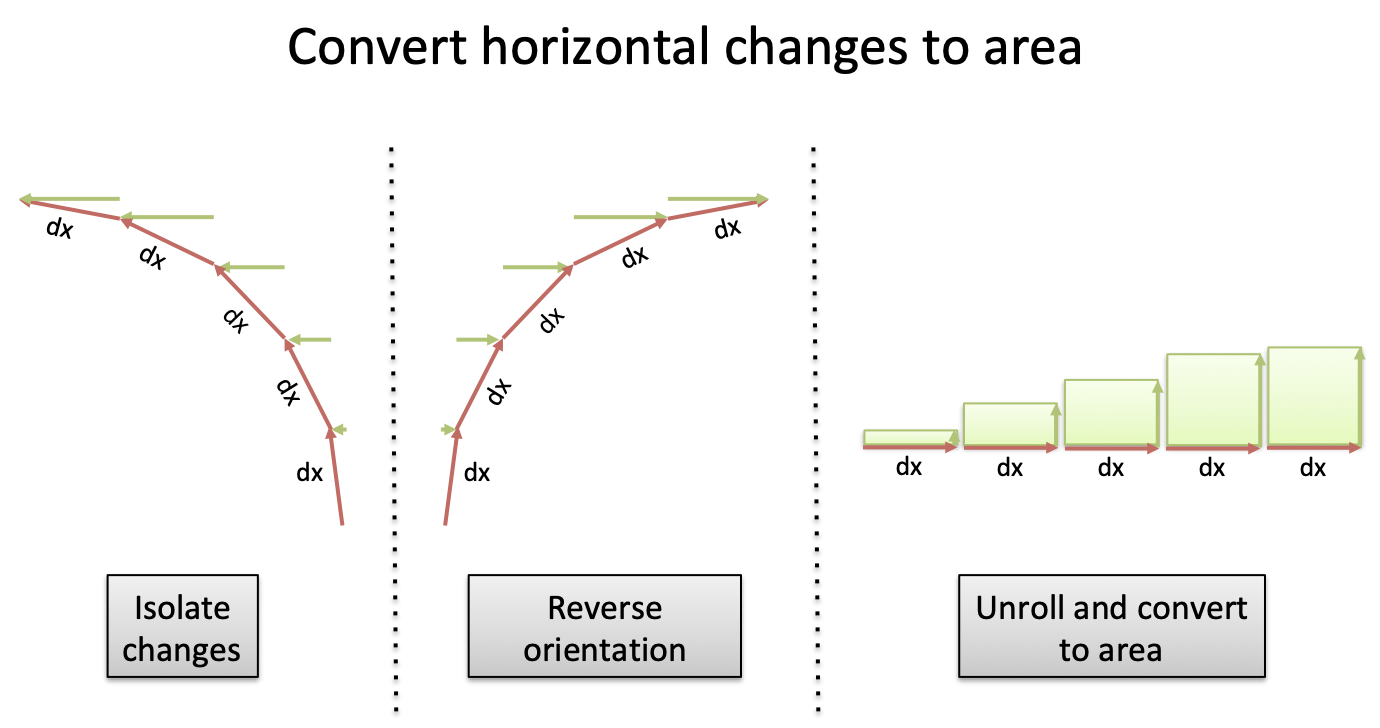
Our excitement to put things in the official format evaporated the intuition of what was happening.

Fundamental Theorem of Calculus

We don’t really talk about the Fundamental Theorem of Calculus anymore. (Is it something I did?)

Instead of adding up all the tiny segments, just do: end point – start point.

The intuition was staring us in the face: $cos(x)$ is the anti-derivative, and tracks the horizontal position, so we’re just taking a difference between horizontal positions! (With awkward negatives to swap the axes.)

That’s the power of the Fundamental Theorem of Calculus. Skip the intermediate steps and just subtract endpoints.

Onward and Upward

Why did I write this? Because I couldn’t instantly figure out:

$ int_0^pi sin(x) dx = 2$

This isn’t an exotic function with strange parameters. It’s like asking someone to figure out $2^3$ without a calculator. If you claim to understand exponents, it should be possible, right?

Now, we can’t always visualize things. But for the most common functions we owe ourselves a visual intuition. I certainly can’t eyeball the 2 units of area from 0 to $pi$ under a sine curve.

Happy math.

Appendix: Average Efficiency

As a fun fact, the “average” efficiency of motion around the top of a circle (0 to $pi$) is: $ frac{2}{pi} = .6366 $

So on average, 63.66% of your path’s length is converted to horizontal motion.

Appendix: Height controls width?

It seems weird that height controls the width, and vice-versa, right?

If height controlled height, we’d have runaway exponential growth. But a circle needs to regulate itself.

$e^x$ is the kid who eats candy, grows bigger, and can therefore eat more candy.

$sin(x) $ is the kid who eats candy, gets sick, waits for an appetite, and eats more candy.

Appendix: Area isn’t literal

The “area” in our integral isn’t literal area, it’s a percentage of our length. We visualized the multiplication as a 2d rectangle in our generic integral, but it can be confusing. If you earn money and are taxed, do you visualize 2d area (income * (1 – tax))? Or just a quantity helplessly shrinking?

Area primarily indicates a multiplication happened. Don’t let team Integrals Are Literal Area win every battle!