Summary: The quadratic formula becomes $x = -b pm sqrt{b^2 – c}$ after two simplifications: divide out $a$, and use the “radius” of the overhanging linear term.

The standard quadratic formula is a lot to remember:

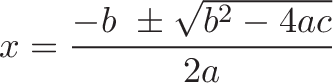
It’s a maze of numbers, letters, and square roots. It’s derived from “completing the square” on a general quadratic equation ($ax^2 + bx + c = 0$). There are several good explanations for the standard formula, here’s my intuition for a variation.

Step 1: Get Rid of A

Here’s our typical starting equation:

First off, why leave $a$ hanging around? Divide that fella out, and get:

In fact, pretend $a$ was never there. You’d combine similar terms ($3x + 4x = 7x$) before doing any other work, right? In a similar way, demand that $x^2$ appear by itself (with no coefficients) before you begin solving.

After dividing any coefficients attached to $x^2$, our equation is in the format:

Ah, that’s a better starting point.

(Note: $b$ and $c$ are what we label the coefficients after all simplifications. For example, when starting with $3x^2 + 6x + 9 = 0$ and simplifying to $x^2 + 2x + 3 = 0$, we’d assign $b=2$ and $c=3$.)

Step 2: Visualize Area

Let’s put on our geometry goggles and assume our quadratic equation refers to area:

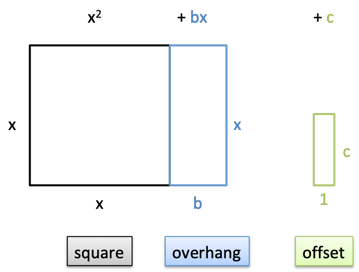
An ongoing insight is that math doesn’t have dimensions or units — just raw quantities. We can decide that in this scenario, every quantity refers to the area of a 2d shape:

• $x^2$ is our square ($x * x$)
• $bx$ is a rectangular overhang ($b * x$)
• $c$ is an offset independent of $x$ ($c * 1$)

Solving the equation means: what length $x$ makes the square, overhang, and offset cancel to zero?

Without an offset ($x^2 + bx = 0$), canceling the total area is easy: just set $x = 0$ or $x = -b$, which collapses one side of the rectangle or the other. (Note that $x$ can have negative length, to cancel the width of the overhang.)

But that offset makes us do extra work.

Step 3: Complete The Square

The trick to canceling the offset is completing the square. First, we move half the overhang to the top of the square:

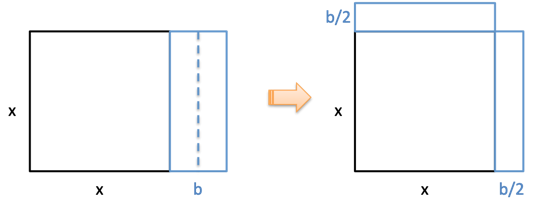
Next, we borrow from the Bank of Zero to fill in the corner:

This part is magic. We can conjure up any quantity if we promise to cancel it later (0 = 1 – 1). So, we borrow material to complete the square, and subtract it again:

Then we can move the extra pieces to the other side:

Let’s fill in some specifics. How big is the corner? Half the overhang ($frac{b}{2}$), squared. Time for some algebra:

Tada! It’s a… slightly less complex quadratic formula.

Step 4: Use the Overhang Radius

This equation is simpler than the quadratic formula, but it’s still gnarly.

$b$ is the width of the full overhang, and $frac{b}{2}$ is the piece we move. Since that’s the plan, why not write things in terms of the part we want? Let’s make $b$ half the overhang:

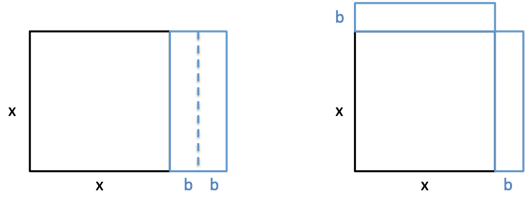
This means our starting equation can be written:

$x^2 + 2bx + c = 0$

Where $b$ is now the “radius” (not full diameter) of the overhang. Completing the square and solving gives us:

Pretty clean!

Example Problem

Let’s solve this equation:

My thought process: first, divide everything by 3. No need to leave things sitting around.

Next, let’s find radius of the overhang. The entire linear coefficient is 2, so the radius is 1. Using the radius formula, we get:

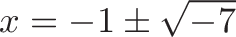
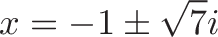
Pretty fast, right?

And to factor the equation (writing it as a set of multiplications) we do:

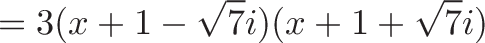
(Verify with wolfram alpha: roots of 3x^2 + 6x + 24 )

Which version of the formula should you use? I’d rather use a simple formula on a simple equation, vs. a complicated formula on a complicated equation.

Appendix: Other Thoughts

Don’t be afraid to rewrite equations

The standard quadratic formula is fine, but I found it hard to memorize. Who says we can’t modify equations to fit our thinking? Ideas like “remove $a$ from the equation” and “use the radius, not diameter” simplifies things, and nicknames like “square, overhang, offset” make the parts memorable.

Practically, we often memorize the equations we’re given, but it doesn’t mean you can’t try a version that makes sense for you.

Why are the roots negative?

It seems strange to have formulas that begin with a negative sign:

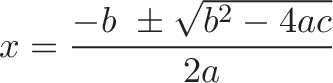
Typically, we need negative lengths to fight the area added by the overhang and make the area collapse to zero. Depending on the values of $a$, $b$ and $c$, the solutions can be positive, negative, zero, or complex.

What is negative area?

This seems to be overlooked in discussions, but when completing the square we can have “negative” area. Negative area is created by sides of imaginary length.

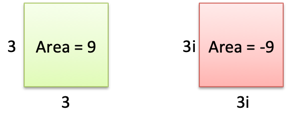
Instead of positive and negative area, I think of colors (green/red). Green area is positive, with real sides (healthy land that grows crops). Red area is negative, with imaginary sides (poisoned land?). The math works out ($3i cdot 3i = 9 i^2 = 9(-1) = -9$) , but our geometric concepts might need some upgrades.

Moving from 2d to 1d

Another aha! moment is realizing what happens when we take a square root. We’re changing out interpretation from 2 dimensions back down to 1:

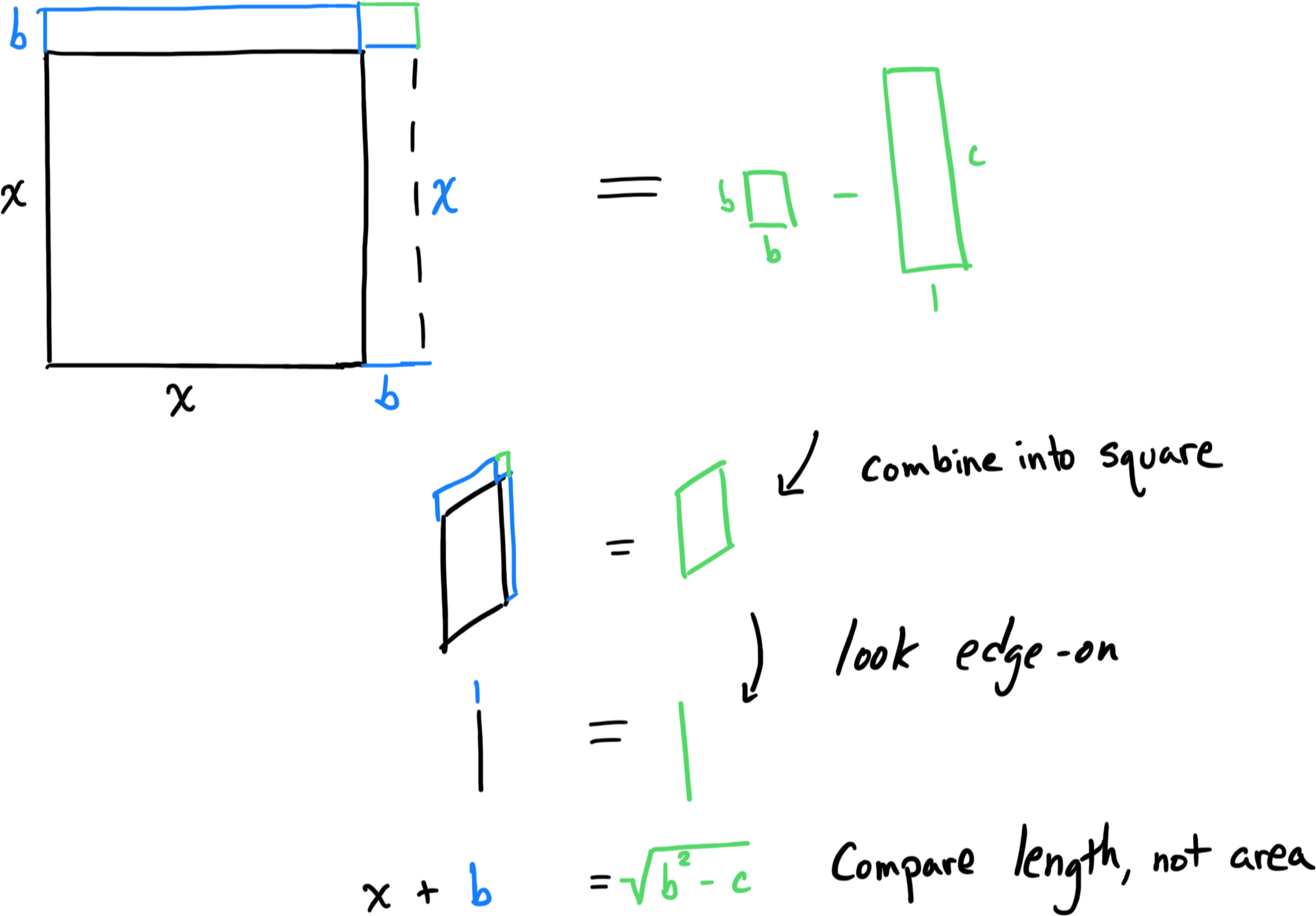
Taking the square root is like looking at our shapes edgewise and comparing the resulting lengths. The equations have no fixed dimensions — just interpretations of quantities — but I like this perspective shift. The unimaginative among us can see completing the square as pure symbol manipulation.

Happy math.